Tổng hợp kiến thức hóa 10: Cấu tạo nguyên tử

Tổng hợp kiến thức hóa 10: CHƯƠNG 1: NGUYÊN TỦ

Bài 1: THÀNH PHÂN NGUYÊN TỬ

– Hạt nhân: Hạt proton (p) mang điện tích dương. Hạt notron (n) không mang điện

– Lớp vỏ là các hạt electron ( e) mang điện tích âm

$\frac{m_{e}}{m_{p}+m_{n}}=2,71 \cdot 10^{-4}=\frac{2,72}{10^{4}} \rightarrow$ tỉ số $m_{\text {vỏ hạt nhân }}: m_{\text {hạt nhân }}$ quá bé $\rightarrow$ Khối lượng của vỏ hạt nhậ quá bé so với hạt nhân $\rightarrow$ KLNT tập trung ở hạt nhân

$\rightarrow \mathrm{m}_{\mathrm{NT}}=\mathrm{m}_{\mathrm{HN}}$

+ Vì nguyên tử trung hòa về điện $\rightarrow$ số hạt $\mathrm{p}=$ số hạt $\mathrm{e}(\mathrm{p}$ và $\mathrm{e}$ mang điện tích)

+ Tổng hạt proton kí hiệu là $Z \rightarrow$ điện tích hạt nhân là $Z^{+}$

+ Tổng hạt notron kí hiệu hiệu là $\mathrm{N}$

– Nguyên tử có khuynh hướng nhường e hay nhận thêm ở lớp vỏ tạo ra ion

$$
\mathrm{R} \rightarrow \mathrm{R}^{+}+1 \mathrm{e} \text { ( Nguyên tử } \mathrm{R} \text { nhường } \mathrm{x} \text { e tạo ra cation } \mathrm{R}^{\mathrm{x}}
$$

Cation ( ion dương)

$\mathrm{R} \rightarrow \mathrm{R}^{\mathrm{x}}+\mathrm{xe}(\mathrm{x}=1,2,3 \mathrm{e}) \rightarrow \mathrm{R}$ thường là kim loại

$$
\mathrm{X}+\mathrm{me} \rightarrow \mathrm{X}^{\mathrm{m}-} \quad(\mathrm{x}=4,3,2,1) \rightarrow \mathrm{X} \text { thường là phi kim }
$$

Anion

VD : Nguyên tử của nguyên tố R có tổng số hạt là 40 ; số hạt mang điện nhiều hơn không mang điện là 12. Xác định nguyên tố $X$ ?

$$
\mathrm{p}+\mathrm{e}+\mathrm{n}=40 \rightarrow \mathrm{Z}+\mathrm{Z}+\mathrm{N}=40 \text { hay }
$$

Ta có hệ

$2 \mathrm{Z}+\mathrm{N}=40$

$2 \mathrm{Z}-\mathrm{N}=12 \rightarrow \mathrm{Z}=13 ; \mathrm{N}=14$

Số Khối $\mathrm{A}$ : $\mathrm{A}=\mathrm{Z}+\mathrm{N}=13+14=27$

Vậy $\mathrm{X}$ là nhôm $(\mathrm{Al})$. ĐTHN là $13^{+}$; ngoài vỏ có $13^{\mathrm{e}}\left(13^{-}\right)$

VD2 : Iôn $\mathrm{R}^{3+}$ tổng số hạt là 79 ; số hạt mang điện nhiều hơn không mang điện là 19 . Xác định nguyên tố $\mathrm{R}$ $2 \mathrm{Z}+\mathrm{N}-3=79$

$2 \mathrm{Z}-\mathrm{N}-3=19 \rightarrow \mathrm{Z}=26 ; \mathrm{N}=30 \rightarrow \mathrm{A}=\mathrm{Z}+\mathrm{N}=56(\mathrm{Fe})$

$\mathrm{R}$ là nguyên tố sắt $(\mathrm{Fe})$

$\mathrm{Fe}$ và $\mathrm{Fe}^{3+} \rightarrow$ số khối của nguyên tử chính là số khối của iôn

VD : Anion $\mathrm{X}^{3-}$ có tổng hạt là 49 ; số hạt mang điện trong nhân ít hơn không mang điện là 1 . Xác đinh nguyên tử $X$

$2 \mathrm{Z}+\mathrm{N}+3=49$

$-\mathrm{Z}+\mathrm{N}=1 \rightarrow \mathrm{Z}=15 ; \mathrm{N}=16 \rightarrow \mathrm{A}=31(\mathrm{P})$

$\mathrm{X}$ là phốt pho

$\rightarrow \mathrm{mP}=\mathrm{mE}+\mathrm{mp}+\mathrm{mN}=15 \cdot \mathrm{m}_{\mathrm{e}}+15 . \mathrm{m}_{\mathrm{p}}+16 . \mathrm{m}_{\mathrm{n}}$ (vì $\mathrm{m}_{\mathrm{e}}$ qua bé so với hạt nhân)

$\rightarrow \mathrm{mP}=\mathrm{mp}+\mathrm{mN}=15 \cdot \mathrm{m}_{\mathrm{p}}+16 \cdot \mathrm{m}_{\mathrm{n}}=5,19 \cdot 10^{-26} \mathrm{~kg}$

Tính $\mathrm{mP}$ ra u

$$
1 \mathrm{u}=1,6605 \cdot 10^{-27} \mathrm{~kg}
$$$$
\text { 5,19. } 10^{-26} \mathrm{~kg} \rightarrow \mathrm{mP}=5,19 \cdot 10^{-26} / 1,6605 \cdot 10^{-27}=31,25 \mathrm{u}
$$

1. Electron

a. Sư tìm ra electron

– Thí nghiệm của Thompson – 1897 ( SGK)

* Đặc tính của tia âm cực:

– Là chùm hạt vật chất có khối lượng, chuyển động với vận tốc lớn.

– Khi không có tác dụng của điện trường và từ trường tia âm cực truyền thẳng.

– Tia âm cực là chùm hạt mang điện tích âm.

$\rightarrow$ Người ta gọi hạt mang điện âm tạo thành tia âm cực là electron (e).

b. Khối lự̛̣g và điện tích electron

$$
\begin{aligned}
& \mathrm{m}_{\mathrm{e}}=9,1094 \cdot 10^{-31} \mathrm{~kg} \\
& \mathrm{q}_{\mathrm{e}}=-1,602 \cdot 10^{-19} \mathrm{C} . \\
& \rightarrow \mathrm{q}_{\mathrm{e}}=1-(\mathrm{dvđt})
\end{aligned}
$$

2. Sự tìm ra hạt nhân nguyên tử

– Thí nghiệm của Rutherford- 1911 (SGK)

* Đạc điểm của hạt nhân :

– Là phần mang điện +, có khối lượng lớn (so với e), nhưng kích thước rất nhỏ (so với nguyên tử).

– Xung quanh hạt nhân có các e tạo nên lớp vỏ. Số e = số $\mathrm{p}$ (vì nguyên tử trung hoà về điện).

Nguyên tử có cấu tạo rỗng, khối lượng nguyên tử hầu như tập trung ở hạt nhân.

3. Cấu tạo của hạt nhân nguyên tử

a. Sự tìm ra proton

$$
\begin{aligned}
& \mathrm{m}_{\mathrm{p}}=1,6726 \cdot 10^{-27} \mathrm{~kg} \\
& \mathrm{q}_{\mathrm{p}}=1,602 \cdot 10^{-19} \mathrm{C}=1+(\mathrm{dvđt})
\end{aligned}
$$

\section{b. Sự tìm ra notron}

$$
\begin{aligned}
& \mathrm{m}_{\mathrm{n}}=1,6748 \cdot 10^{-27} \mathrm{~kg} \approx \mathrm{m}_{\mathrm{p}} \\
& \mathrm{q}_{\mathrm{n}}=0
\end{aligned}
$$

c. Cấu tạo hạt nhân nguyên tử

– Được cấu thành bởi các $\mathrm{p}$ và $\mathrm{n}$

$$
\text { số } \mathrm{p}=\text { số đơn vị đthn = số e }
$$

II. Kích thước và khối lượng của nguyên tử

1. Kích thước

-Đơn vị : $1 \mathrm{~nm}=10^{-9} \mathrm{~m}$ (nm: nanomet)

$$
1 \AA=10^{-10} \mathrm{~m} \text { ( } \mathrm{A}^{0} \text { : Amstrong) }
$$

– Nguyên tử của các nguyên tố khác nhau có kích thước khác nhau.

– Đường kính nguyên tử cỡ $10^{-1} \mathrm{~nm}$ nhỏ nhất là Hiđro,

$$
\mathrm{r}_{\mathrm{H}}=0,53 \AA=0,053 \mathrm{~nm}
$$

– Đường kính hạt nhân cỡ $10^{-5} \mathrm{~nm} \rightarrow$ kích thước nguyên tử lớn hơn hạt nhân khoảng $10^{4}$ lần.

Đường kính $\mathrm{e}, \mathrm{p}, \mathrm{n}$ cỡ $10^{-8} \mathrm{~nm}$.

$$
\mathrm{V}_{\mathrm{NT}}=\frac{4}{3} \cdot \Pi \cdot r^{3} ; \quad \mathrm{D}=\mathrm{m}_{\mathrm{NT}} / \mathrm{V}(\mathrm{gam} / \mathrm{cm})
$$

\section{Khối lượng}

– Đơn vị khối lượng nguyên tử: u, đvC

$$
\begin{aligned}
& 1 u=\frac{1}{12} m_{C-12}=\frac{1}{12} \cdot 19,9265 \cdot 10^{-27} \mathrm{~kg} \\
& \Leftrightarrow 1 u=1,6605 \cdot 10^{-27} \mathrm{~kg}
\end{aligned}
$$

– Đổi : $\mathrm{m}_{\mathrm{p}}=$ ? u $\quad \mathrm{m}_{\mathrm{n}}=$ ? u $\quad \mathrm{m}_{\mathrm{e}}=$ ? $\mathrm{u}$

$\rightarrow \mathrm{m}_{\mathrm{NT}}(\mathrm{u})=$

\section{Hạt nhân nguyên tử}

\section{Bài 2: HẠT NHÂN NGUYÊN TỦ}

\section{1. Điện tích hạt nhân.}

– Hạt nhân có $Z$ proton $\rightarrow$ điện tích hạt nhân là $Z^{+} \rightarrow$ số đơn vị điện tích hạt nhân bằng $Z$.

– Nguyên tử trung hoà về điện $\rightarrow$ số $\mathrm{p}=$ số $\mathrm{e}$.

– Kết luận: số đơn vị điện tích hạt nhân $\mathrm{Z}=$ số $\mathrm{p}=$ số e

\section{Số khối}

– Số khối: số khối $\mathrm{A}=\mathrm{Z}+\mathrm{N}$

$\mathrm{Z}$ : tổng số hạt $\mathrm{p}, \mathrm{N}$ : tổng số hạt $\mathrm{n}$

– Số đơn vị ĐTHN $\mathrm{Z}$ và số khối $\mathrm{A}$ : đặc trưng cho hạt nhân và cũng là đặc trưng cho nguyên tử.

Vì: biết $\mathrm{A}, \mathrm{Z} \rightarrow$ số $\mathrm{n}=\mathrm{N}=\mathrm{A}-\mathrm{Z}$

$$
Z \rightarrow \text { số } \mathrm{p}=\text { số e }
$$

\section{KHNT ${ }_{Z}^{A} X$}

VD: Nguyên tử của nguyên tố $X$ có tổng hạt là 34 , số hạt mang điện trong nhân ít hơn không mạng điện là 1

a. Viết KHNT

b. Tính KLNT ra ( gam), ( u)

\section{Ta có}

$2 \mathrm{Z}+\mathrm{N}=\mathbf{3 4}$

$-\mathrm{Z}+\mathrm{N}=\mathbf{1} \rightarrow \mathrm{Z}=\mathbf{1 1} ; \mathrm{N}=\mathbf{1 2} \rightarrow \mathrm{A}=\mathbf{2 3}$

a. KHNT ${ }_{11}^{23} \mathrm{Na}$; ĐTHN là $11^{+}$; số ĐV ĐTHN 11

b. $\mathrm{mNa}=\mathrm{m}_{\mathrm{p}}+\mathrm{m}_{\mathrm{n}}=11 \cdot \mathrm{M}_{\mathrm{p}}+12 \cdot \mathrm{m}_{\mathrm{n}}=3,85 \cdot 10^{-26} \mathrm{~kg}=3,85 \cdot 10^{-23}$ gam

$$
\mathbf{m N a}=3,85 \cdot 10^{-26} \mathrm{~kg} / \mathrm{u}=23,18 \mathrm{u}
$$

\section{Nguyên tố hoá học}

\section{1. Định nghĩa:}

– Nguyên tố hoá học là những nguyên tử có cùng điện tích hạt nhân.

– VD : các nguyên tử có $\mathrm{Z}=12$ đều thuộc nguyên tố $\mathrm{Mg}$. chúng đều có $12 \mathrm{p}$ ở hạt nhân và $12 \mathrm{e}$ ở lớp vỏ. Nguyên tố Hidro có 3 nguyên tử : ${ }_{1} \mathrm{H}^{1}$ ( proti-P); ${ }_{1} \mathrm{H}^{2}$ ( đotơri) ( D) ${ }_{1} \mathrm{H}^{3}$ ( triti- T)

$$
\text { Nuyên tố oxi có } 3 \text { nguyen tử : }{ }_{8} \mathrm{O}^{16} ;{ }_{8} \mathrm{O}^{17} ;{ }_{8} \mathrm{O}^{18}
$$

\section{Số hiệu nguyên tử.}

Số đvđthn nguyên tử của một nguyên tố được gọi là số hiệu nguyên tử của nguyên tố đó, kí hiệu là Z

\section{Kí hiệu nguyên tử}<smiles>[Y][V]</smiles>

KHNT cho ta biết :

số hiệu nguyên tử $\mathrm{Z}$ = số đthn = số $\mathrm{p}$ = số e, số $\mathrm{n}=\mathrm{A}-\mathrm{Z}$

\section{III. Đồng vị}

VD Xác định số $\mathrm{p}, \mathrm{n}$ trong các đồng vị của Hidro

$\begin{array}{llll}\text { Đồng vị } & { }_{1}^{1} \mathrm{H} & { }_{1}^{2} \mathrm{H}\left({ }_{1}^{2} \mathrm{D}\right) & { }_{1}^{3} \mathrm{H}\left({ }^{3} \mathrm{~T}\right) \\ \text { Tên } & \text { proti } & \text { Đoteri } & \text { Triti } \\ \mathrm{Z} & 1 & 1 & 1 \\ \mathrm{n} & 0 & 1 & 2 \\ \mathrm{~A} & 1 & 2 & 3\end{array}$

– Các đồng vị của cùng một nguyên tố hoá học là những nguyên tử có cùng số $\mathrm{p}$ nhưng khác nhau số $\mathrm{n}$ do đó số khối A của chúng khác nhau

– Các đồng vị được xếp vào cùng một ô trong BTH.

– Các đồng vị bền $(\mathrm{Z}<82)$ thì: $1 \leq \mathrm{N} / \mathrm{Z} \leq 1,5$

\section{Nguyên tử khối và nguyên tử khối trung bình của các nguyên tố hoá học}

\section{Nguyên tử khối}

$\mathrm{Na}=23$ (u)

– VD : xét nguyên tử hidro

– $\mathrm{m}_{\mathrm{H}}=1,6735 \cdot 10^{-27} \mathrm{~kg} \approx 1 \mathrm{u}$

nguyên tử khối : $\frac{\mathbf{1 u}}{\mathbf{u}}=\mathbf{1}$

– Kết luận : NTK là khối lượng tương đối của nguyên tử cho biết nguyên tử đó nặng gấp bao nhiêu lần đơn vị khối lượng nguyên tử.

– ta có $\mathrm{KLNT}=\Sigma \mathrm{m}_{\mathrm{p}}+\Sigma \mathrm{m}_{\mathrm{n}}+\Sigma \mathrm{m}_{\mathrm{e}}$.

$\mathrm{m}_{\mathrm{e}}<<\mathrm{m}_{\mathrm{p}}, \mathrm{m}_{\mathrm{n}}$ nên :

$\mathrm{m}_{\text {ng tú }} \approx \sum \mathrm{m}_{\mathrm{p}}+\sum \mathrm{m}_{\mathrm{n}}$

vì $\mathrm{m}_{\mathrm{p}} \approx \mathrm{m}_{\mathrm{n}} \approx 1 \mathrm{u}$ nên $\mathrm{NTK}=\mathrm{A}$

– Áp dụng : xác định NTK của nguyên tử P, $\mathrm{S}$

\section{Nguyên tử khối trung bình.}

– Trong BTH, nguyên tử khối của các nguyên tố là nguyên tử khối trung bình, vì các nguyên tố đều có nhiều đồng vị.

– Giả sử nguyên tố $\mathrm{X}$ có các đồng vị có số khối lần lượt là $\mathrm{A}_{1}, \mathrm{~A}_{2}, \mathrm{~A}_{3} \ldots$ và thành phần $\%$ tương ứng là $\mathrm{x}_{1}, \mathrm{x}_{2}$, $\mathrm{x}_{3} \ldots$ thì:

$$
\overline{\mathrm{A}}_{\mathrm{X}}=\frac{\mathrm{X}_{1} \cdot \mathrm{n}_{1}+\mathrm{X}_{2} \cdot \mathrm{n}_{2}+\ldots+\mathrm{X}_{\mathrm{i}} \cdot \mathrm{n}_{\mathrm{i}}}{100}
$$

VD1: Cacbon tự nhiên là hỗn hợp 2 đồng vị C-12, C-13. Trong đó C-12 chiếm 98,9\%. Tính NTK TB của C. $\overline{\mathrm{A}}_{\mathrm{C}}=\frac{12.98,9+13 \cdot(100-98,9)}{100}=12,011$

$M_{T b}=\left(x . M_{1}+y \cdot M_{2}\right) /(x+y)$

VD2: Tỉ lệ số nguyên tử của hai đồng vị $\mathrm{A}, \mathrm{B}$ trong tự nhiên của cùng một nguyên tố là 27:23. Đồng vị A có $35 \mathrm{p}, 44 \mathrm{n}$; đồng vị $\mathrm{B}$ có nhiều hơn $\mathrm{A} 2 \mathrm{n}$. Tính nguyên tử khối trung bình của nguyên tố.

Kí hiệu nguyên tử đồng vị là

$$
\begin{array}{lr}
{ }_{35}^{79} \mathrm{~A} & { }_{35}^{81} \mathrm{~B} \\
27 & : 23
\end{array}
$$

$\overline{\mathrm{A}}=\frac{79.27+81.23}{27+23}=79,92$

VD3: Trong tự nhiên, đồng $(\mathrm{Cu})$ có 2 đồng vị bền là $\mathrm{Cu}-63$ và $\mathrm{Cu}-65$, trong đó $\mathrm{Cu}-65$ chiếm $27 \%$ về số nguyên tử. Tính \% về khối lượng của $\mathrm{Cu}-63$ trong $\mathrm{Cu}_{2} \mathrm{O}$ (cho $\mathrm{O}=16$ ).

$$
\overline{\mathrm{A}}_{\mathrm{Cu}}=\frac{63.73+65.27}{100}=63,54
$$

Cứ $1 \mathrm{~mol} \mathrm{Cu}_{2} \mathrm{O}$ có $2 \mathrm{~mol} \mathrm{Cu}$ (hỗn hợp đồng vị)

$\Rightarrow$ Số mol Cu-63 = 0,73.2 = 1,46 mol

$$
\% \mathrm{~m}_{\mathrm{Cu}-63}=\frac{1,46 \cdot 63}{63,54 \cdot 2+16} \cdot 100 \%=64,29 \%
$$

 

Bài 3: SỤ๋ CHUYỂN ĐộNG CỦA ELECTRON TRONG NGUYÊN TỦ̉. OBITAN NGUYÊN TỦ

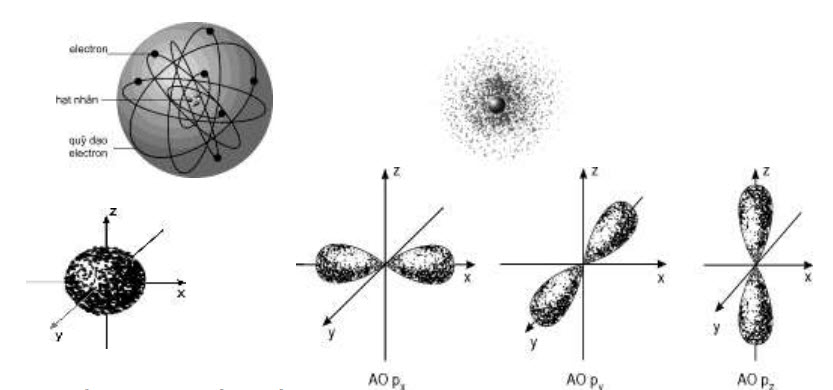
SỰ CHUYỂN ĐộNG CỦA CÁC E TRONG NGUYÊN TỬ:

1. Mô hình hành tinh nguyên tử :

– Các e chuyển động theo các quỹ đạo xác định xung quanh hạt nhân như trái đất quay xung quanh mặt trời.

– Mô hình mẩu hành tinh nguyên tử đơn giản dễ hiểu nhưng giải thích thoả đáng các tính chất của nguyên tử.

2. Mô hình hiện đại về sự chuyển động của các e trong nguyên tử . Obitan nguyên tử :

a. Sự chuyển động của các e trong nguyên tử:

– Các e chuển động rất nhanh xung quanh hạt nhân nhưng không theo một quỹ đạo xác định mà tạo thành “đám mây” e.

\section{b. Obitan nguyên tử:}

– Obitan nguyên tử là khu vực không gian xung quanh hạt nhân mà tại đó xác suất có mặt (tìm thấy) các e khoảng $90 \%$

– Obitan không có giới hạn nhưng để đơn giản người ta có thể biểu diễn obitan có đường giới hạn cho dễ hình dung.

\section{c. Hình dạng obitan nguyên tử :}

– Obitan $\mathrm{s}$ có dạng hình cầu.

– Obitan p có dạng hình số 8 nổi.

– Obitan d, f có hình dạng phức tạp.

LỚP ELECTRON VÀ PHÂN LỚP ELECTRON

Lớp electron

– Trong nguyên tử các electron được sắp xếp thành từng lớp, từ trong ra ngoài.

-Các electron trên cùng một lớp có mức năng lượng gần bằng nhau. -Những electron ở gần nhân có mức năng lượng thấp, liên kết với hạt nhân chặt chẽ hơn. Ngược lại các electron ở xa nhân liên kết với hạt nhân yếu có mức năng lượng cao.

– Số thứ tự lớp electron được ghi bằng số nguyên $\mathrm{n}=1,2, \ldots, 7$

$\mathrm{n}=\begin{array}{llllllll}1 & 2 & 3 & 4 & 5 & 6 & 7\end{array}$

Tên lớp: K L M N O P Q.

Lớp $\mathrm{K}$ là lớp gần nhân nhất, các electron lớp này liên kết với hạt nhân chặt chẽ nhất và có mức năng lượng thấp nhất.

\section{Phân lớp electron}

– Các electron trên cùng 1 phân lớp có mức năng lượng bằng nhau.

– Các phân lớp ký hiệu bằng chữ cái thường theo thứ tự năng lượng tăng dần: s, p, d, f. Ta nói phân lớp s, phân lớp $\mathbf{p} . .$.

Lớp $\mathrm{K}(\mathrm{n}=1)$ có 1 phân lớp. Kí hiệu $1 \mathbf{s}$

Lớp L ( $\mathrm{n}=2)$ có 2 phân lớp. Kí hiệu 2 s, 2p

Lớp M (n=3) có 3 phân lớp. Kí hiệu 3s, 3d, 3p

Lớp $\mathrm{N}(\mathrm{n}=4)$ có 4 phân lớp. Kí hiệu 4s, 4p, 4d, $4 \mathbf{f}$

Các e ở phân lớp $\mathrm{s}$ được gọi là electron $\mathrm{s}$.

Các e ở phân lớp $\mathrm{p}$ được gọi là electron $\mathrm{p}$.

Vậy phân lớp n có $n$ phân lớp $(n \leq 4)$

III. SỐ ELECTRON TỐI ĐA TRONG MỘT PHÂN LỚP, MỘT LỚP

\section{Số e tối đa trong một phân lớp}

– Phân lớp s chứa tối đa $2 \mathrm{e}$.

– Phân lớp p chứa tối đa $6 \mathrm{e}$.

– Phân lớp d chứa tối đa $10 \mathrm{e}$.

– Phân lớp f chứa tối đa $14 \mathrm{e}$.

Các phân lớp đã chứa tối đa e: $\mathrm{s}^{2}, \mathrm{p}^{6}, \mathrm{~d}^{10}, \mathrm{f}^{14}$ được gọi là các phân lớp bão hoà.

\section{Số e tối đa trong 1 lớp}

Vậy: Lớp thứ $\mathbf{n}$ có tối đa $2 \mathrm{n}^{2}$ electron $(\mathrm{n} \leq 4)$.

VD: xác định số lớp e của các nguyên tử $\mathrm{N}(\mathrm{Z}=14)$; $\mathrm{Mg}(\mathrm{Z}=12)$.

$\mathrm{N}(\mathrm{Z}=7): 2 / 5 \rightarrow \mathrm{N}$ có 2 lớp e

$\mathrm{Mg}(\mathrm{Z}=12): 2 / 8 / 2 \rightarrow \mathrm{Mg}$ có 3 lớp e.

\section{Số e tối đa trong 1 obitan}

– Người ta kí hiệu obitan nguyên tử bặng 1 ô vuông gọi là ô lượng tử.

– Mỗi obitan chỉ chứa tối đa 2e.

4. Số obitan trong một phân lớp và một lớp

– Phân lớp s chứa tối đa 1 obitan

– Phân lớp p chứa tối đa 3 obitan

– Phân lớp d chứa tối đa 5 obitan

– Phân lớp f chứa tối đa 7 obitan

\section{Bài 4: CÁC SỐ LƯợNG TỬ}

1. Số lượng tử chính n: qui định mức năng lượng của 1 electron (hay lớp electron), các electron trên cùng 1 lớp có mức năng lượng gần bằng nhau.

2. Số lượng tử phụ I: qui định kiểu và hình dạng obitan (hay phân lớp), các electron trên cùng 1 phân lớp có mức năng lượng bằng nhau. Với mỗi giá trị của $n$, thì 1 nhận các giá trị nguyên từ 0 đến (n-1)

Vậy ở lớp thứ $\mathrm{n}$ có $\mathrm{n}$ phân lớp $(\mathrm{n} \leq 4)$

3. Số lượng tử từ $\mathbf{m}$ : qui định hướng obitan trong không gian

Với mỗi giá trị của 1 thì $m$ nhận các giá trị nguyên từ $-1 ; \ldots ; 0 ; \ldots+1$

Vậy phân lớp s có $1 \mathrm{AO}$, phân lớp p 3AO, phân lớp d có $5 \mathrm{AO}$, phân lớp f có 7AO VD: Một electron trên phân lớp $\mathrm{s}$ thuộc lớp thứ 2 , kí hiệu là: $2 \mathrm{~s}$ và có 3 số lượng tử là $\mathrm{n}=2, \mathrm{l}=0, \mathrm{~m}=0$

d. Số lưọ̣ng tử spin s: qui định chiều tự quay của electron $\mathrm{s}=+1 / 2$ (spin-up); s = -1/2 (spin-down)

VD: E cuối cùng của một nguyên tử phân bố như sau:

Quy ước: số lương tử $m$ nhận giá trị từ thấp đến cao.

Tổng kết

$$
3 p \quad(n=3 ; \mathrm{l}=1 ; \mathrm{m}=+1 ; \mathrm{s}=+1 / 2)
$$

Câu 1. Cho tổ hợp 4 số lượng tử sau, tổ hợp nào không tồn tại? Giải thích.
a. $\mathrm{n}=3 ; \mathrm{l}=2 ; \mathrm{m}=2 ; \mathrm{s}=+1 / 2$
b. $\mathrm{n}=4 ; \mathrm{l}=3 ; \mathrm{m}=-3 ; \mathrm{s}=+1 / 2$
c. $\mathrm{n}=4 ; \mathrm{l}=2 ; \mathrm{m}=-2 ; \mathrm{s}=-1 / 2$

Câu 2. Cho biết bộ bốn số lượng tử của electron chót cùng trên nguyên tử của các nguyên tố A, B, D lần lượt là:
A: $\mathrm{n}=2,1=1, \mathrm{~m}=1, \mathrm{~s}=+1 / 2$.
B: $\mathrm{n}=3, \mathrm{l}=1, \mathrm{~m}=1, \mathrm{~s}=-1 / 2$
$\mathrm{D}: \mathrm{n}=4,1=0, \mathrm{~m}=0, \mathrm{~s}=+1 / 2$

Xác định các nguyên tử $\mathrm{A}, \mathrm{B}, \mathrm{D}$. Viết cấu hình electron đầy đủ và cấu hình orbital.

Câu 3. Xác định bộ bốn số lượng tử của các elctron trong nguyên tử $\mathrm{Mg}(\mathrm{Z}=12), \mathrm{Cu}(\mathrm{Z}=29)$

Câu 4. Nguyên tử của nguyên tố $\mathrm{A}$ có bộ bốn số lượng tử của electron chót cùng là: $\mathrm{n}=4, \mathrm{~m}=0,1=0, \mathrm{~s}=$ +1/2. Xác định $\mathrm{A}$. Viết cấu hình electron, xác định vị trí của A trong bảng HTTH.

Câu 5. Biết e có năng lượng cao nhất của nguyên tử $X$ đặc trưng bằng 4 số lượng tử $\left(\mathrm{n}=4,1=2, \mathrm{~m}=2, \mathrm{~m}_{\mathrm{s}}=\right.$ -1/2). Xác định cấu hình e.

Câu 6. Electron cuối cùng của ion $\mathrm{A}^{-}, \mathrm{B}^{2+}$ đều có cùng bộ bốn số lượng tử. Biết rằng bốn số lượng tử đó thoả mãn: $n . m=3$ và $\ell+s=1 / 2$. Viết cấu hình electron của $\mathrm{A}, \mathrm{B}$.

Bài 5. CẤU HÌNH ELECTRON NGUYÊN TỬ

SÁP XẾP ELECTRON TRONG VỎ NGUYÊN TỬ

Các nguyên lí, qui tắc

a. Nguyên lí Pauli

– Mỗi obitan chỉ chứa tối đa 2 electron. Khi obitan chứa tối đa 2e thì spin của chúng phải ngược dấu (gọi là $2 \mathrm{e}$ ghép đôi), nếu obitan chỉ chứa 1e thì e đó là e độc thân.

b. Nguyên lí vững bền

Ở trạng thái cơ bản, trong nguyên tử, các electron chiếm lần lượt các $\mathrm{AO}$ có mức năng lượng từ thấp tới cao.

1s 2s 2p 3s 3p 4s 3d 4p 5s 4d 5p 6s…

c. Qui tắc Hund

Trong 1 phân lớp, các electron phân bố vào các $\mathrm{AO}$ sao cho tổng spin là cực đại (số e độc thân cực đại)

Cấu hình electron

* Cấu hình electron nguyên tử biểu diễn sự phân bố electron trên các phân lớp thuộc các lớp khác nhau

* Quy ước:

– Số thứ tự lớp là $1,2,3 \ldots$.

– Phân lớp ký hiệu s, p, d, f

– Số electron được nghi bằng chỉ số ở phía trên, bên phải ký hiệu của phân lớp $\left(\mathrm{s}^{2}, \mathrm{p}^{2} \ldots\right)$

* Cách viết cách hình electron

– Xác định số electron của nguyên tử

– Nắm vững các nguyên lý, quy tắc

– Viết theo thứ tự các phân lớp và theo thứ tự các lớp

VD: ${ }_{19} \mathrm{~K} \quad 1 \mathrm{~s}^{2} 2 \mathrm{~s}^{2} 2 \mathrm{p}^{6} 3 \mathrm{~s}^{2} 3 \mathrm{ps}^{6} 4 \mathrm{~s}^{1}$

${ }_{26} \mathrm{Fe} 1 s^{2} 2 s^{2} 2 p^{6} 3 s^{2} 3 p^{6} 4 s^{2} 3 d^{6}$

Hay $[\mathrm{Ar}] 3 \mathrm{~d}^{6} 4 \mathrm{~s}^{2}$

\section{H $\mathbf{1 s}^{1}$}

2He $1 s^{2}$

${ }_{3} \mathbf{L i} 1^{2} 2 s^{1}$

${ }_{4 B} \operatorname{Be} s^{2} 2 s^{2} 2 p^{1}$

${ }_{5} B \quad 1 s^{2} 2 s^{2} 2 p^{1}$

C: $1 s^{2} 2 s^{2} 2 p^{2}$ hay [He] $2 s^{2} 2 p^{2}$

$\mathbf{N}: 1 s^{2} 2 s^{2} 2 p^{3}$ hay [He] $2 s^{2} 2 p^{3}$

3. Đặc điểm lớp electron ngoài cùng

– Đối với mọi nguyên tử, số electron lớp ngoài cùng tối đa là 8. Các nguyên tử có $8 \mathrm{e}$ lớp ngoài cùng đều bền vững, hầu như không tham gia phản ứng hoá học, thuộc nguyên tố khí hiếm (trừ He tuy có 2e lớp ngoài cùng nhưng cũng thuộc nguyên tố khí hiếm).

– Các nguyên tử có 1, 2, 3 electron lớp ngoài cùng thường thuộc nguyên tố kim loại (trừ $\mathrm{H}, \mathrm{He}, \mathrm{B})$. Các nguyên tử kim loại dễ nhường 1, 2, 3 electron lớp ngoài cùng tạo thành ion dương.

– Các nguyên tử có 5, 6, 7 electron thường thuộc nguyên tố phi kim. Các nguyên tử phi kim có khuynh hướng nhận 3, 2, 1 electron vào lớp ngoài cùng, tạo thành ion âm.

– Các nguyên tử có 4 electron lớp ngoài cùng có thể thuộc nguyên tố kim loại hoặc phi kim. Bài tập áp dụng

1. Viết cấu hình electron của các nguyên tố:

$\mathrm{Z}=20,21,22,24,29$ => kim loại, phi kim, khí hiếm, số electron độc thân

2. Viết cấu hình electron nguyên tử, biểu diễn sự phân bố các electron vào các ô lượng tử, biết rằng electron cuối cùng điền vào lớp vỏ có các số lượng tử như sau:
a. $\mathrm{n}=2 ; \mathrm{l}=1 ; \mathrm{m}=0 ; \mathrm{s}=+1 / 2$
b. $\mathrm{n}=2 ; \mathrm{l}=1 ; \mathrm{m}=0 ; \mathrm{s}=-1 / 2$
c. $\mathrm{n}=3 ; \mathrm{l}=1 ; \mathrm{m}=-1 ; \mathrm{s}=-1 / 2$

Bài 6. Năng Lưọ̣ng Của Electron Trong Nguyên Tử Hidro Và Các Ion Một Điện Tử

1) Năng lượng của electron trong nguyên tử $\mathrm{H}$ và các ion tương tự nguyên tử $\mathrm{H}$ (các ion có 1 electron):


2) Tổng quát (theo Slater):

trong đó:

$$
E_{n, l}=-13,6 Z^{* 2} / n^{* 2}(e V) \text {. }
$$

$Z^{*}$ : số điện tích hiệu dụng $=(\mathrm{Z}-\mathrm{b})$, với $b$ là hằng số chắn.

$n^{*}$ : số lượng tử hiệu dụng.

a) Số lượng tử hiệu dụng

Tùy thuộc vào số lượng tử chính $\mathrm{n}, \mathrm{n}^{*}$ được xác định như sau:

b) Hằng số chắn

Để tính b, người ta chia các AO thành các nhóm sau: (1s); (2s,2p); (3s,3p); (3d); (4s,4p); (4d); $\mathrm{S}_{1 \mathrm{~s}}=0,3$

$\mathrm{S}_{2 \mathrm{~s}, 2 \mathrm{p}}=0,35$. ( số e ở phân lớp s,p -1) + 0,85. ( số e lớp sát trong) + 1. ( số e còn lại lớp trong)

$\mathrm{S}_{\mathrm{d}}=0,35$. ( số e ở phân lớp $\left.\mathrm{d}-1\right)+1$. ( tất cả số e còn lại)

VD: Xét nguyên tử $C: 1 s^{2} 2 s^{2} 2 p^{2}$

Đối với electron trên obitan $1 \mathrm{~s}: \mathrm{b}=0,3 ; \mathrm{Z}^{*}=6-0,3=5,7$.

Đối với electron trên obitan 2s hoặc $2 \mathrm{p}: \mathrm{b}=3 \cdot 0,35+2 \cdot 0,85=2,75 ; \mathrm{Z}^{*}=3,25$.

Năng lượng :

$\mathrm{E}_{1 \mathrm{~s}}=-13,6 \cdot(5,7)^{2}=-441,8(\mathrm{eV})$

$\mathrm{E}_{2 \mathrm{~s}}=\mathrm{E}_{2 \mathrm{p}}=-13,6 \cdot(3,25)^{2} / 4=-35,9(\mathrm{eV})$

Tổng năng lượng các electron trong nguyên tử $\mathrm{C}$ :

$\mathrm{E}_{\mathrm{C}}=2 \mathrm{E}_{1 \mathrm{~s}}+2 \mathrm{E}_{2 \mathrm{~s}}+2 \mathrm{E}_{2 \mathrm{p}}=-1027,2 \mathrm{eV}$.

– Năng lượng ion hóa thứ nhất là năng lương cần thiết để tách một e ra khỏi nguyên tử.

$\mathrm{Li}(\mathrm{Z}=3): 1 \mathrm{~s}^{2} / 2 \mathrm{~s}^{1} \rightarrow \mathrm{E}_{\mathrm{Li}}=2 \mathrm{E}_{1 \mathrm{~s}}+\mathrm{E}_{2 \mathrm{~s}}=2 .(-99,14)-5,747=-204.034 \mathrm{eV}$

$-204.034 \mathrm{eV} .1,602 \cdot 10^{-19}$ J. $10^{-3} \mathrm{KJ} .6,023.10^{23}(\mathrm{KJ} / \mathrm{mol})=$

$1 \mathrm{eV}=1,602 \cdot 10^{-19} \mathrm{~J}$

$1 \mathrm{~mol}=\mathrm{N}_{\mathrm{A}}=6,023 \cdot 10^{23}$ ( nguyên tử, phân tử, ion)

$\mathrm{S}_{2 \mathrm{~s}}=0,35 \cdot 0+0,85 \cdot 2=1,7 \rightarrow \mathrm{E}_{2 \mathrm{~s}}=-13,6(3-1,7)^{2} / 2^{2}=-5,746 \mathrm{eV}$

$$
\begin{aligned}
& \mathrm{S}_{1 \mathrm{~s}}=0,3 \rightarrow \mathrm{E}_{1 \mathrm{~s}}=-13,6(3-0,3)^{2} / 1^{2}=-99,14 \mathrm{eV} \\
& \mathrm{Li} \rightarrow \mathrm{Li}^{+}+1 \mathrm{e} \quad \mathrm{I}_{1}=\mathrm{E}_{\mathrm{Li}}-\mathrm{E}_{\mathrm{Li}}=2 \mathrm{E}_{1 \mathrm{~s}}-\left(2 . \mathrm{E}_{1 \mathrm{~s}}+\mathrm{E}_{2 \mathrm{~s}}\right)=+5,746 \mathrm{eV} \\
& \mathrm{Li}^{+} \rightarrow \mathrm{Li}^{2+}+1 \mathrm{e} \mathrm{I}_{2}=\mathrm{E}_{\mathrm{Li} 2+}-\mathrm{E}_{\mathrm{Li}+}=-122,4-(-2 \mathrm{x} 99,14)=+75,88 \mathrm{eV} \\
& \mathrm{Li}^{2+} \rightarrow \mathrm{Li}^{3+}+1 \mathrm{e} ; \mathrm{I}_{3}=\mathrm{E}_{\mathrm{Li}}^{3+}-\mathrm{E}_{\mathrm{Li}^{2+}}^{2+}=0-(-122,4)=+122,4 \mathrm{eV} \\
& \mathrm{E}_{\mathrm{Li}^{2+}}^{2+}=-13,6 . \mathrm{Z}^{2} / \mathrm{n}^{2}=-13,6.3^{2} / 1^{2}=-122,4 \mathrm{eV} \\
& \mathrm{VD}: \mathrm{Li} \rightarrow \mathrm{Li}^{+}+1 \mathrm{e} \text { Vậy } \mathrm{I}_{1}=\mathrm{E}_{\mathrm{Li+}}-\mathrm{E}_{\mathrm{Li}} \\
& \mathrm{E}_{\mathrm{Li}}=\mathrm{E}_{2 \mathrm{~s}}+2 \mathrm{E}_{1 \mathrm{~s}} \\
& \mathrm{Li}^{+} \rightarrow \mathrm{Li}^{2+}+1 \mathrm{e}
\end{aligned}
$$

\section{Bài 7: SỤ๋ PHÓNG XẠ}

\section{KHỐI LƯợNG HẠT NHÂN – SỰ HỤT KHỐI – NĂNG LƯợNG LIÊN KẾT HẠT NHÂN 1. Khối lượng hạt nhân – Độ hụt khối}

Theo lí thuyết thì $\quad \mathrm{m}_{\mathrm{h} . \mathrm{n}}=\sum \mathrm{m}_{\mathrm{p}}+\sum \mathrm{m}_{\mathrm{n}}=\mathrm{Z} \cdot \mathrm{m}_{\mathrm{p}}+\mathrm{N} \cdot \mathrm{m}_{\mathrm{n}}$

Theo thực nghiệm thì $\mathrm{m}_{\mathrm{h} . \mathrm{n}}<\mathrm{Z} \cdot \mathrm{m}_{\mathrm{p}}+\mathrm{N} \cdot \mathrm{m}_{\mathrm{n}}$

$\rightarrow \quad$ Độ hụt khối của hạt nhân: $\Delta \mathrm{m}=\mathrm{Z} \cdot \mathrm{m}_{\mathrm{p}}+\mathrm{N} \cdot \mathrm{m}_{\mathrm{n}}-\mathrm{m}_{\mathrm{h.n}(\mathrm{tn})}$

\section{Năng lượng liên kết hạt nhân}

$\mathrm{E}_{\mathrm{lk}}=\Delta \mathrm{m} \cdot \mathrm{c}^{2}\left(\mathrm{c}=3 \cdot 10^{8} \mathrm{~m} / \mathrm{s}\right)=931,5 \cdot \Delta \mathrm{m}\left(\mathrm{MeV} / \mathrm{c}^{2}\right)$, biết $1 \mathrm{MeV}=10^{6} \mathrm{eV}=10^{6} \cdot 1,602 \cdot 10^{-19} \mathrm{~J}$

VD: Hạt nhân ${ }_{2}^{4} \mathrm{He}$ có khối lượng hạt nhân theo thực nghiệm: 4,0015u. Tính năng lượng liên kết hạt nhân He

Độ hụt khối: $\Delta \mathrm{m}=4,032-4,0015=0,0305 \mathrm{u}=0,0305.931,5 \mathrm{MeV} / \mathrm{c}^{2}$.

Người ta thường đưa năng lượng liên kết $\mathrm{E}_{\mathrm{k}}$ về năng lượng liên kết trên 1 nucleon, gọi là năng lượng liên kết riêng. $\quad E=\frac{E_{1 k}}{A}$

Năng lượng liên kết riêng $\mathrm{E}$ càng lớn, hạt nhân càng bền vững.

VD: Tính năng lượng liên kết và năng lượng liên kết riêng của hạt nhân ${ }_{26}^{54} \mathrm{Fe}$ và ${ }_{92}^{238} \mathrm{U}$, so sánh độ bền hai hạt nhân, biết rằng $\mathrm{m}_{\mathrm{Fe}}=53,956 \mathrm{u} ; \mathrm{m}_{\mathrm{U}}=238,125 ; \mathrm{m}_{\mathrm{p}}=1,0073 \mathrm{u} ; \mathrm{m}_{\mathrm{n}}=1,0087 \mathrm{u}$.

1. Phóng xạ tự nhiên: Một số hạt nhân không bền tự phân rã phóng ra những tia có thành phân phần phức tạp

\section{Thành phần của tia phóng xạ}

Xét tác dụng của từ trường lên tia phóng xạ, người ta phân biệt 3 loại tia phóng xạ:

a.Tia $\alpha$ : Phóng ra hạt $\alpha$ hay hạt nhân nguyên tử $\mathrm{He}\left({ }_{2}^{4} \mathrm{He}\right.$ ) có đặc điểm

+ Tốc độ khoảng $20000 \mathrm{Km} / \mathrm{s}$

+ Khả năng đâm thâu kém nhưng khả năng ioon hóa cao

b.Tia $\beta$ : gồm những vi tử là negatron (hay electron) (ký hiệu $\beta^{-}$hay ${ }_{-1}^{0} e$ ) hoặc những vi tử là positron (ký hiệu $\beta^{+}$hay ${ }_{1}^{0} e$ ).

+ Tốc độ khoảng: $280000 \mathrm{Km} / \mathrm{s}$

+ Khả năng đâm thâu cao ( vài $\mathrm{mm}$ nhôm)

c. Tia $\gamma$ : gồm những vi tử trung hòa, thực chất là các dòng photon (tia $\gamma$ có cùng bản chất với ánh sáng).

+ Tộc độ cao, năng lương cao.

+ Khả năng đâm xuyên cao ( khoản $20 \mathrm{~cm}$ chì)

\section{3. Định luật chuyển dịch phóng xạ}

Trong một phản ứng phóng xạ thì số khối và điện tích được bảo toàn VD: Hoàn thành các phản ứng sau:
a. ${ }_{13}^{27} \mathrm{Al}+{ }_{2}^{4} \mathrm{He} \longrightarrow{ }_{0}^{1} n+X$
b. ${ }_{15}^{30} P \longrightarrow{ }_{0}^{1} e+X$
c. ${ }_{80}^{196} \mathrm{Hg} \stackrel{+n}{\longrightarrow} X \stackrel{-\beta}{\longrightarrow} Y$
d. ${ }_{92}^{238} U \stackrel{{ }^{+n}}{\longrightarrow} X \underset{-\beta}{\longrightarrow} Y \underset{-\beta}{\longrightarrow} T$
e. ${ }_{92}^{235} U \stackrel{+n}{\longrightarrow} X \rightarrow{ }_{56}^{141} \mathrm{Ba}+X+3 n$
f. ${ }_{88}^{224} R a \longrightarrow X+\alpha$
g. ${ }_{84}^{216} \mathrm{Po} \longrightarrow X+\alpha$
h. ${ }_{84}^{216} \mathrm{Po} \longrightarrow X+\beta^{-}$

\section{4. Định luật phân rã phóng xạ}
a. Định luật:
$\mathbf{N}=\mathbf{N o}^{\mathrm{e}} \mathbf{e}^{-\mathrm{kt}}$

(1)

$\mathrm{N}_{\mathrm{o}}$ : số hạt nhân phóng $\mathrm{xạ}$ có tại thời điểm đầu $(\mathrm{t}=0)$

$\mathrm{N}$ : số hạt nhân đó còn lại ở thời điểm $\mathrm{t}$ đang xét

$\mathrm{k}$ : hằng số phân rã phóng xạ.

Hay $\mathrm{t}=\frac{1}{k} \ln \frac{A^{0}}{A} ; \mathrm{t}=\frac{1}{k} \ln \frac{N^{0}}{N} ; \mathrm{t}=\frac{1}{k} \ln \frac{m^{0}}{m}$

b. Chu kỳ bán hủy $\left(\mathrm{t}_{1 / 2}\right)$ : là thời gian để chất phân hủy hết $1 / 2$ lượng chất ban đầu.

$$
t_{1 / 2}=\ln 2 / k=0,693 / k
$$

c. Độ phóng xạ (hoạt độ phóng xạ)

* Độ phóng xạ $\mathrm{A}$ của một mẫu phóng xạ là một đại lượng bằng số phân rã trong một đơn vị thời gian.

$$
\mathrm{A}=-\mathrm{dN} / \mathrm{dt}=\mathrm{k} . \mathrm{N}
$$

Đơn vị phóng xạ được đo bằng Curi $(\mathrm{Ci})$.

$1 \mathrm{Ci}=3,7.10^{10}$ phân rã / giây $=3,7.10^{10} \mathrm{~Bq}$ (Becquerel).

* Người ta đã xác định được rằng: trong khí quyển, trong mỗi cơ thể động thực vật đang sống, cứ 1 giây, trong 1 gam cacbon có 15,3 phân rã ${ }^{14} \mathrm{C}$. Khi cơ thể này chết đi, tốc độ phân hủy đó giảm dần với chu kỳ bán hủy 5730 năm.

Từ (1), (2), (3) suy ra:

$$
\mathrm{t}=\left(\mathrm{t}_{1 / 2} / 0,693\right) \cdot \ln \left(\mathrm{N}_{\mathrm{o}} / \mathrm{N}\right)=\left(\mathrm{t}_{1 / 2} / 0,693\right) \cdot \ln \left(\mathrm{R}_{0} / \mathrm{R}\right)
$$

trong đó:

$\mathrm{R}_{0}$ : 15,3 phân rã ${ }^{14} \mathrm{C}$ trong 1 giây trong 1 gam cacbon

$\mathrm{R}$ : số phân rã ${ }^{14} \mathrm{C}$ trong 1 giây trong 1 gam cacbon ở thời điểm $\mathrm{t}$.

\section{Năng lượng liên kết hạt nhân – Phản ứng hạt nhân}

a. Năng lượng liên kết hạt nhân $(\Delta \mathbf{E})$. Biết $1 \mathrm{u}=931,5\left(\mathrm{MeV} / \mathrm{c}^{2}\right)$

$$
\Delta \mathrm{E}=\Delta \mathrm{m} \cdot \mathrm{c}^{2}=\Delta \mathrm{m} \cdot 931,5(\mathrm{M} \mathrm{eV})
$$

trong đó, $\Delta \mathrm{m}=\left(\mathrm{Z} \cdot \mathrm{m}_{\mathrm{p}}+\mathrm{N} \cdot \mathrm{m}_{\mathrm{n}}\right)-\mathrm{m}_{\text {hạt nhân }}$

$\Delta \mathrm{E} / \mathrm{A})$ : năng luợng liên kết riêng hay năng lượng liên kết trung bình của 1 nucleon. $\Delta \mathrm{m}$ : gọi là độ hụt khối. $\rightarrow$ Tổng khối lương các hạt nucleon trong hạt nhân bao giờ cũng lớn hơn khối lượng nguyên tử.

\section{b. Phản ứng hạt nhân}

Sự tương tác của hai hay nhiều hạt dẫn đến tạo thành nguyên tố mới (và có thể có thêm phần khác) được gọi là phản ứng hạt nhân.

Trong phản ứng hạt nhân, số khối và điện tích được bảo toàn.

HIỆN TƯợNG PHÓNG XẠ VÀ PHẢN ỨNG HẠT NHÂN

Các loại hạt phóng xạ

Sự phóng xạ:

a) Các hạt nhân nặng không bền (U, Th, Pu, Po, Ra…) liên tục tự phát ra các tia không nhìn thấy gọi là tia phóng xạ: $\alpha\left({ }_{2}^{4} \mathrm{He}\right) ; \beta\left({ }_{-1}^{0} \mathrm{e}\right) ; \gamma$ (bức xạ)

Ví dụ: $\quad{ }_{83}^{210} \mathrm{Bi} \rightarrow{ }_{84}^{210} \mathrm{Po}+{ }_{-1}^{0} \mathrm{e} \quad$ và $\quad{ }_{84}^{210} \mathrm{Po} \rightarrow{ }_{82}^{206} \mathrm{~Pb}+{ }_{2}^{4} \mathrm{He}$

b) Định luật chuyển dịch phóng xạ (các định luật bảo toàn số khối và định luật bảo toàn proton):

$$
{ }_{Z}^{A} \mathrm{X} \rightarrow{ }_{Z-2}^{A-4} \mathrm{Y}+{ }_{2}^{4} \mathrm{He} \quad \text { và } \quad{ }_{Z}^{A} \mathrm{X} \rightarrow{ }_{Z+1}^{A} \mathrm{Y}+{ }_{-1}^{0} \mathrm{e}
$$

Phóng xạ $\gamma$ không làm thay đổi nguyên tố

\section{Các loại phản ứng hạt nhân:}

\section{a. Phản úng đơn giản:}

Ví dụ: phản ứng Rutherford ${ }_{2}^{4} \mathrm{He}+{ }_{7}^{14} \mathrm{~N} \rightarrow{ }_{8}^{17} \mathrm{O}+{ }_{1}^{1} \mathrm{p}$ (thí nghiệm tìm ra proton)

$$
\text { phản ứng Chadwick } \quad{ }_{2}^{4} \mathrm{He}+{ }_{4}^{9} \mathrm{Be} \rightarrow{ }_{6}^{12} \mathrm{C}+{ }_{0}^{1} \mathrm{n} \text { (thí nghiệm tìm ra notron) }
$$

\section{b. Phản úng phân hạch:}

Ví dụ: ${ }_{0}^{1} \mathrm{n}+{ }_{92}^{235} \mathrm{U} \rightarrow \mathrm{X}+\mathrm{Y}+3 \mathrm{n}$ (Bom nguyên tử, nguyên tắc lò phản ứng hạt nhân)

\section{c. Phản úng nhiệt hạch:}

Ví dụ: ${ }_{1}^{2} \mathrm{H}+{ }_{1}^{2} \mathrm{H} \rightarrow{ }_{2}^{4} \mathrm{He} \quad$ (Nguyên tắc bom hidro)

\section{3. Động học quá trình phóng xạ:}

a/ Tốc độ phóng xạ: $\mathrm{v}=-\frac{d N}{d t}=\mathrm{k} \cdot \mathrm{N}$ (k là hằng số phóng xạ, $\mathrm{N}$ là số nguyên tử tại thời điểm xét)

b/ Hằng số phóng xạ: $\mathrm{k}=\frac{\ln 2}{t_{1 / 2}}=\frac{0,693}{t_{1 / 2}}$

c/ Chu kỳ bán hủy $\left(\mathrm{t}_{1 / 2}\right)$ : là thời gian để lượng chất ban đầu mất đi một nửa $\left(\mathrm{a} / 2\right.$ hay $\left.\mathrm{N}_{0} / 2\right)$

Quan hệ: $\mathrm{k}=\frac{1}{t} \ln \frac{N_{0}}{N_{t}} \quad\left(\mathrm{~N}_{0}\right.$ là số hạt nhân phóng xạ tại thời điểm ban đầu, $\mathrm{N}_{\mathrm{t}}$ là số hạt nhân đó còn lại tại thời điểm $\mathrm{t}$ đang xét, $\mathrm{t}$ là thời gian phóng xạ)

Hay $k=\frac{1}{t} \ln \frac{m_{0}}{m}$ hay $k=\frac{1}{t} \ln \frac{A_{0}}{A}$

\section{BT Cơ bản}

1. Hoàn thành phản ứng hạt nhân sau:

a. ? $\rightarrow{ }_{82}^{206} \mathrm{~Pb}+{ }_{2}^{4} \mathrm{He}$

b. ${ }_{94}^{239} \mathrm{Pu} \rightarrow ?+{ }_{2}^{4} \mathrm{He}$

c. ? $+{ }_{1}^{2} \mathrm{D} \rightarrow 2{ }_{2}^{4} \mathrm{He}$

d. ${ }_{9}^{17} \mathrm{~F} \rightarrow{ }_{8}^{17} \mathrm{O}+$ ? 2. Hoàn thành phản ứng hạt nhân sau:

$$
{ }_{92}^{238} \mathrm{U} \stackrel{(1)}{\longrightarrow} ?+{ }_{90}^{234} \mathrm{Th} \stackrel{(2)}{\longrightarrow}{ }_{91}^{234} \mathrm{~Pa}+\text { ? } \stackrel{(3)}{\longrightarrow} \beta^{-}+\text {? } \stackrel{(4)}{\longrightarrow}{ }_{2}^{4} \mathrm{He}+\text { ? }
$$

3. ${ }_{92}^{238} U$ là một chất phóng xạ. Sau nhiều lần phóng xạ liên tiếp mà thời gian sống của các hạt nhân trung gian là ngắn đủ để có thể bỏ qua sự có mặt của nó trong sản phẩm chuyển hóa. Phương trình phóng xạ như sau: ${ }_{92}^{238} \mathrm{U} \rightarrow{ }_{82}^{206} \mathrm{~Pb}+\mathrm{x} \alpha+\mathrm{y} \beta^{-}$

a. Xác định hệ số $x, y$.

b. Thực nghiệm chi biết tại thời gian khảo sát một mẫu đá Urani có tỉ lệ khối lượng ${ }_{92}^{238} U$ còn lại và khối lượng ${ }_{82}^{206} \mathrm{~Pb}$ là 0,0453 . Biết $\mathrm{T}_{1 / 2}$ của ${ }_{92}^{238} U$ là 4,55921.10 năm. Hãy tính tuổi cảu mẫu đá trên

4. Urani trong thiên nhiên có hai đồng vị là ${ }_{92}^{238} U$ ( chiếm $99,28 \%$ có $T_{1 / 2}$ là 4,5.10 năm) và ${ }_{92}^{235} U$ ( chiếm $0,72 \%$ có $T_{1 / 2}$ là $7,1.10^{8}$ năm). Tính tốc độ phân rã của mỗi đồng vị trên có trong $10 \mathrm{gam}_{3} \mathrm{U}_{8}$ mới điều chế?

5. Sự phân hủy phóng xạ của ${ }_{90}^{232} T h$ tuân theo phản ứng bậc một. Nghiên cứa phóng xạ của thori đioxit người ta biết $\mathrm{T}_{1 / 2}=1,39 \cdot 10^{10}$ năm. Hãy tính số hạt $\alpha$ bị bức xạ trong 1 gam thori đioxit.

\section{BTAD.}

6. Trong chuỗi phóng xạ tự nhiên bắt đầu với ${ }_{90}^{232} \mathrm{Th}$ và kết thúc là đồng vị bền ${ }_{82}^{208} \mathrm{~Pb}$

a. Tính số phân hủy $\beta$ xảy ra trong chuỗi này.

b. Trong toàn chuỗi có bao nhiêu năng lượng được giải phóng

$$
\text { Cho }{ }_{2}^{4} \mathrm{He}=4,00260 \mathrm{u} ;{ }_{82}^{208} \mathrm{~Pb}=207,97664 \mathrm{u} ;{ }_{90}^{232} \mathrm{Th}=232,03805 \mathrm{u}, 1 \mathrm{u}=931,5 \mathrm{MeV} / \mathrm{c}^{2}
$$

7. Dựa vào công thức tính năng lượng Slater. Hãy tính năng lượng ion hóa thứ nhất và thứ 2 của $\mathrm{Mg}($ $\mathrm{Z}=12)$

8. Dựa vào công thức tính năng lương Slater. Hãy cho biết cấu hình của $\mathrm{Ni}^{2+}$ nào bền hơn?

Biết Ni( $\mathrm{Z}=28)$

Cách 1: $1 s^{2} 2 s^{2} 2 p^{6} 3 s^{2} 3 p^{6} 3 d^{8}$

Cách 2: $1 s^{2} 2 s^{2} 2 p^{6} 3 s^{2} 3 p^{6} 3 d^{6} 4 s^{2}$

9. Khi nghiên cứu một cỗ vật có nguồn gốc hữu cơ chứa $1 \mathrm{mg}$ Cacbon, người ta thấy rằng tỉ lệ đồng vị $\frac{{ }^{14} C}{{ }^{12} C}$ của mẫu là $1,2 \cdot 10^{-14}$

a. Có bao nhiêu nguyên tử ${ }^{14} \mathrm{C}$ trong mẫu.

b. Tốc độ phân rã của ${ }^{14} \mathrm{C}$ trong mẫu bằng bao nhiêu?

c. Tuổi của mẫu vật nghiên cứa bằng bao nhiêu?

Biết $\mathrm{T}_{1 / 2}$ của ${ }^{14} \mathrm{C}$ là 5730 năm. Hoạt độ phóng xạ riêng của cacbon thời chưa có hoạt động hạt nhân của con người là $277 \mathrm{~Bq} / \mathrm{Kg} ; 1 \mathrm{~Bq}=1$ phân rã/giây.

10. Giả sử đồng vị phóng $x a ̣{ }_{92}^{238} U$ phóng $x a ̣$ ra các hạt $\alpha$ và $\beta$ với $T_{1 / 2}=5.10^{9}$ năm tạo thành ${ }_{82}^{206} \mathrm{~Pb}$

a. Có bao nhiêu hạt $\alpha$ và $\beta$ phóng thích ra?

b. Một mẫu đá chứa $47,6 \mathrm{mg}{ }_{92}^{238} U$ và $30,9 \mathrm{mg}{ }_{82}^{206} \mathrm{~Pb}$. Hãy tính tuổi của mẫu đá đó.

11. Hạt nhân liti có khối lượng 7,01601u. Hãy tính năng lượng liên kết riêng của hạt nhân liti? Cho khối lượng proton và nơtron lần lượt là $1,00724 \mathrm{u} ; 1,00862 \mathrm{u}$. Biết $1 \mathrm{u}=931,5 \mathrm{MeV} / \mathrm{c}^{2}$.

12. Hoạt tính phóng xạ của ${ }_{84}^{210} \mathrm{Po}$ giảm đi $6,85 \%$ sau 14 ngày. Xác định hằng số tốc độ phân rã, chu kì bán hủy và thời gian để cho nó bị phân rã $75 \%$. 13. Tìm số hạt $\alpha$ và $\beta$ được phóng ra từ phóng xạ ${ }_{92}^{238} U$ thành nguyên tố $X$. Biết rằng nguyên tử của nguyên tố $\mathrm{X}$ có electron cuối được đặc trưng bởi bốn số lượng tử $\mathrm{n}=6 ; l=1 ; \mathrm{m}_{l}=0 ; \mathrm{m}_{\mathrm{s}}=+1 / 2$. Tỉ lệ giữa các hạt không mang điện và mang điện trong hạt nhân nguyên tử $X$ là 1,5122 . (Quy ước: từ $-I$ đến $+l$ ).

14. ${ }^{14} \mathrm{C}$ là đồng vị kém bền, phóng xạ $\beta^{-}$, có chu kì bán hủy 5700 năm.

a. Hãy viết phương trình phóng xạ của ${ }^{14} \mathrm{C}$.

b. Tính tuổi cổ vật có tỉ lệ ${ }^{14} \mathrm{C} /{ }^{12} \mathrm{C}$ là 0,125 .

c. Tính độ phóng xạ của một người nặng $80,0 \mathrm{~kg}$. Biết rằng trong cơ thể người đó có $18 \%$ khối lượng là cacbon, độ phóng xạ của cơ thể sống là $0,277 \mathrm{~Bq}$ tính theo 1,0 gam cacbon tổng số.

15. Tính năng lượng liên kết hạt nhân theo $\mathrm{kJ} / \mathrm{mol}$ đối với mỗi hạt nhân sau:
a. ${ }_{10}^{20} \mathrm{Ne}$
b. ${ }_{27}^{59} \mathrm{Co}$
c. ${ }_{46}^{106} \mathrm{~Pa}$

Khối lượng hạt nhân lần lượt là: $19,9925 \mathrm{u} ; 58,9332 \mathrm{u} ; 105,9032 \mathrm{u}$.

b. Trong số các hạt nhân trên, hạt nhân nào có năng lượng liên kết quy về mỗi nucleon lớn nhất?

16. Cho $\mathrm{E}=\Delta \mathrm{m}$. $\mathrm{C}^{2}$ biết $1 \mathrm{u}=931,5 \mathrm{MeV} / \mathrm{c}^{2}$

Cho khối lượng của Đoteri ${ }_{1}^{2} H$ là $\mathrm{mĐ}=2,0135$ u và $\mathrm{He}$ là $\mathrm{m}_{\mathrm{He}}=4,0015 \mathrm{u}$

Lấy $\mathrm{m}_{\mathrm{p}}=1,0073 \mathrm{u} ; \mathrm{m}_{\mathrm{n}}=1,0087 \mathrm{u}$.

Tính năng lượng liên kết qui về mỗi nucleon của hai nguyên tử trên.

17. Một mẫu radon phóng xạ $\alpha$ có độ phóng xạ 7,0 $10^{4} \mathrm{Bp}$. Sau 6,6 ngày độ phóng xạ còn $2,1 \cdot 10^{4} \mathrm{Bp}$. Xác định chu kì bán hủy của Radon.

18. Có một loại rác phóng xạ có chu kỳ bán hủy là 200 năm chứa đựng trong một congtainer và chôn sâu xuống lòng đất. Hỏi sau bao nhiêu lâu thì độ phóng xạ giảm từ $6,5 \cdot 10^{12}$ phân rã trong một phút xuống còn $3,0.10^{-3}$ phân rã trong một phút để không còn tác hại nữa.

19. Đồng vị iôt – 131 phóng xạ được dùng dưới dạng Natri iôtua để điều chế ung thư vòm họng. Nó phân hủy theo kiểu $\beta$ với chu kỳ bán hủy 8,05 ngày.

a. Viết phương trình phản ứng.

b. Tính độ phóng xạ trong một phút nếu mẫu vật chứa $1 \mu \mathrm{g}$ iôt – 131 .

20. Một mảnh gỗ thu được trong hang động có độ phóng xạ của cacbon -14 chỉ bằng 0,636 lần độ phóng xạ của gỗ mới đẫn ngày nay. Biết chu kì bán hủy của C -14 là 5730 năm. Tính niên đại của mảnh gỗ.

21. Năm 1947 người ta tìm thấy cuốn kinh Cữu Ước của người Do Thái. Cuốn sách bọc bởi sợi lanh. Độ phóng xạ của ${ }^{14} \mathrm{C}$ trong sợi lanh vào khỏang 11 phân rã phóng xạ trong một phút đối với mỗi gam sợi. Biết chu kì bán hủy của ${ }^{14} \mathrm{C}$ là 5730 năm và độ phóng xạ của ${ }^{14} \mathrm{C}$ trong vật liệu sống là 14 phân rã/phút. Hãy tính tuổi của cuốn cuốn kinh.

22. Một mẫu quặng Urani chứa $4,64 \mathrm{mg}{ }^{238} U$ và $1,22 \mathrm{mg}{ }^{206} \mathrm{~Pb}$. Biết chu kỳ bán hủy của ${ }^{238} U$ là $4,51.10^{9}$ năm. Xác định tuổi của quặng đó.

Tải file ở phần comment